При расчете конструкций зданий и сооружений инженер выполняет построение расчетной модели из конечных элементов и, как правило, модель подходит только для одного расчетного случая. В заметке рассмотрим сложности при работе со стальной балочной клеткой, на которую опирается монолитная железобетонная плита.
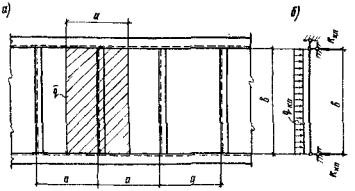
Представим задачу: необходимо выполнить расчет несущей способности стальной балки, если известны конструкция балок (длина, шаг) и конструкция покрытия. По большинству рекомендаций инженер без труда вычислит грузовую площадь, составит расчетную схему в виде балки, приложит нагрузку и получит изгибающий момент, который и пойдет для проверки сечения.
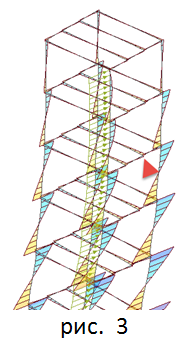
Если необходимо учесть действие ветра на раму, то стоит собрать многоэтажную раму или все здание, приложить нагрузку ветра, получив при этом новые значения моментов. При креплении балок к колоннам с помощью жестких узлов отличие от значений одиночной балки будут существеннее. Итак, собрав схему, мы получим пространственную рамную конструкцию, загрузим ее также по грузовой площади, получим моменты и проверим сечение (рис. 2). Самое интересное начинается, когда в задании фигурирует неравномерная боковая нагрузка или, чаще всего, сейсмика.
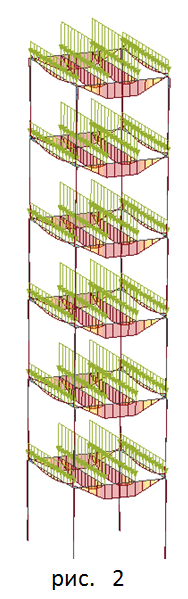
Роль связевых элементов в здании со стальным каркасом нередко выполняют монолитные плиты перекрытия. Если не моделировать их, то получим изгибающий момент балок из плоскости, который непременно повлияет на проверку сечения (получится изгиб в двух плоскостях). Произвольная боковая нагрузка на схему и усилия от ее действия приведены на рис. 3. Изгибающие моменты в такой конструкции из плоскости кажутся не естественными, поскольку плита раскрепляет балку по всей длине, значит любые горизонтальные выгибы балки должны быть компенсированы жесткостью плиты. Пробуем смоделировать перекрытие по балкам с помощью традиционных пластинчатых элементов – КЭ тонкой оболочки. Присваиваем жесткость плите, анализируем результаты (см. рис. 4). В качестве инструмента по расчету конструкции подойдет практически любая программа, работающая на методе конечных элементов.
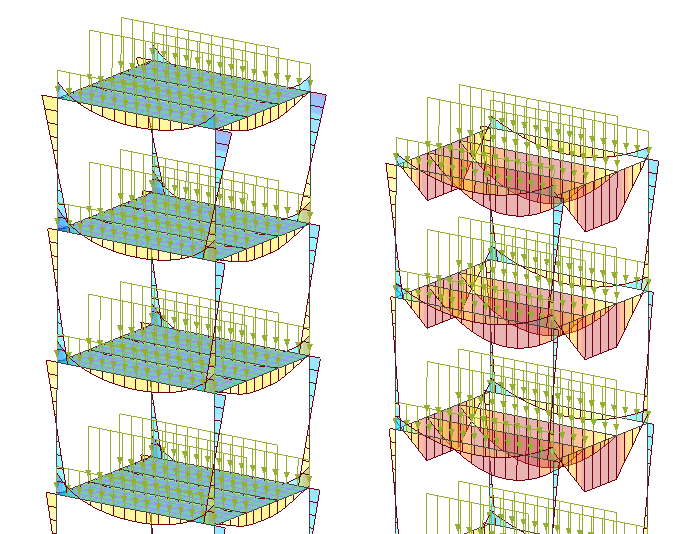
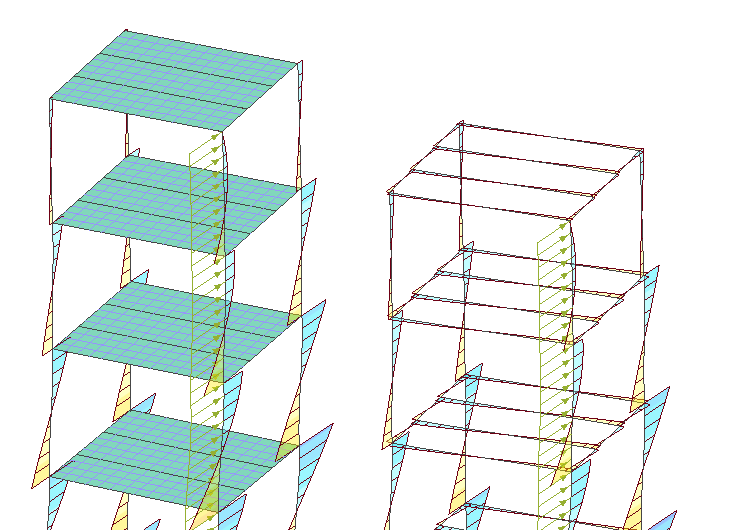
В итоге получаем следующие результаты расчета: изгибающий момент из плоскости балок стал равен нулю, но вместе с этим уменьшился и момент балки в плоскости! Это произошло по причине того, что плита теперь работает совместно с балками. О совместной работе сталежелезобетона в нашей стране долгое время существовали только рекомендации, не так давно появились нормы: СП 266.1325800.2016 «Конструкции сталежелезобетонные». В нормах говорится о работе плиты с учетом профлиста, дается понятие жесткой арматуры и, что важно для нашей задачи, как работает стальная балка с монолитной плитой. Также приводятся разные схемы работы конструкции, описываются разные особенности совместной работы. Так, в нормах сказано:
«4.4.4.8 Расчет поперечного сечения следует выполнять по стадиям, число которых определяется числом частей сечения, последовательно включаемых в работу. Для каждой части сечения действующие напряжения следует определять суммированием их по стадиям работы.»
В нашем случае изгибающий момент, согласно нормам, должен быть разделен также на стадии и складываться из:

Отсюда мы делаем вывод: рассматривать конструкцию с реальной жесткостью плиты не совсем правильно, поскольку момент в расчетной модели делится одновременно и на балку, и на плиту. В реальности же плита начинает работу только на второй стадии, причем я уверен, что не весь пролет будет работать совместно с балкой, а вероятно, только одна из частей. Алгоритмом работы с таким конструкциями может начинаться с вычисления момента в балке без работы плиты, а затем подбор сечения будет уточнен уже с учетом железобетонной конструкции.
Итак, приходим к выводу что ввод плиты в схему помогает устранить выгибы балок из плоскости, но вместе с этим уменьшает и изгибающий момент в плоскости конструкции. Получается, что здесь необходим такой пластинчатый конечный элемент, который бы в своей плоскости работал (растяжение-сжатие), а при изгибе «выключался». Такой элемент есть, он называется – пластинчатый КЭ плоского напряжения (балка-стенка). Также есть еще пластинчатый КЭ плоской деформации, но в данном случае он нам он не подходит, т.к. имеет продольное усилие, перпендикулярное плоскости пластине и применяется для толстых плит (соизмеримых с пролетом по толщине). Для нашей задачи мы используем элемент балка-стенка и получаем следующие результаты:
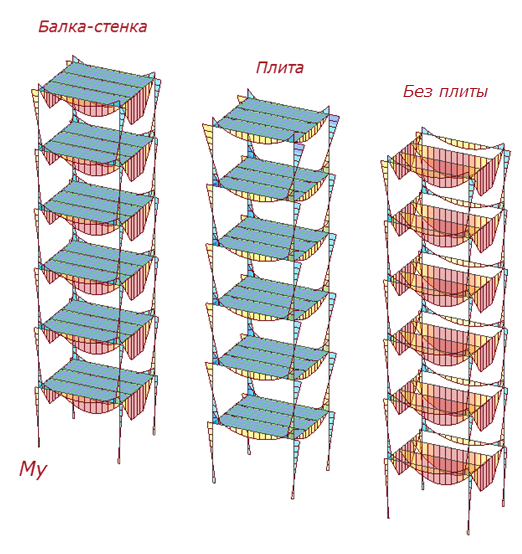
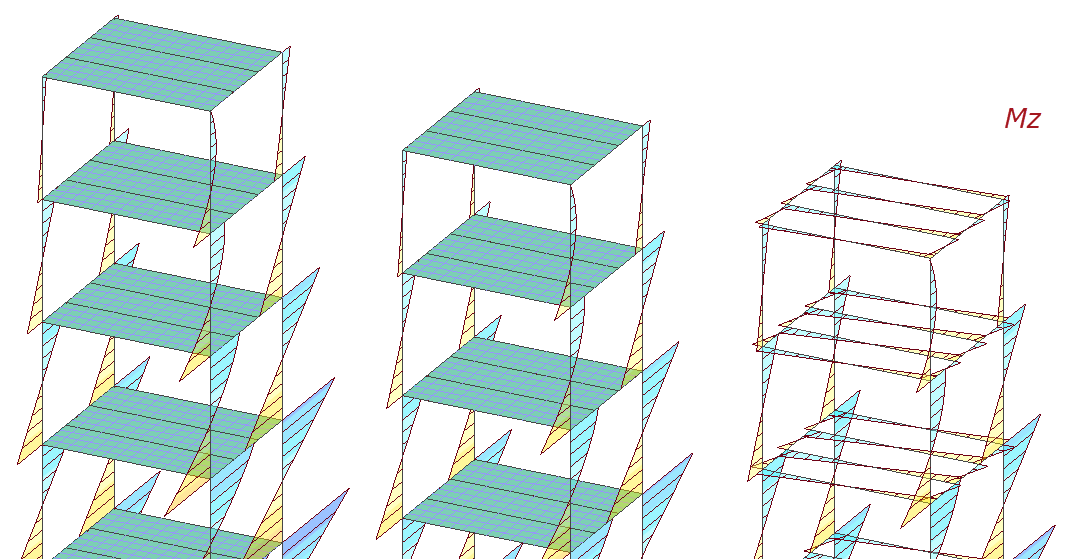
Изгибающие моменты в плоскости при использовании балки-стенки получились аналогичные схеме при полном отсутствии плит. Моменты из плоскости при боковой неравномерной нагрузке отсутствуют так же, как и в схеме с обычными пластинами. Нагрузка на балку-стенку не прикладывается, загружать необходимо балки!
Таким образом, использование балки-стенки дает возможность учесть работу перекрытия при выгибах балок. Это значит, что их жесткость будет учтена при всех боковых нагрузках на схему, в том числе динамических. Балка-стенка не позволит учесть требование норм по совместной работе железобетонного перекрытия и стальной балки. Вся нагрузка будет предаваться на балки, на учет жесткости плиты будет «идти в запас» несущей способности.
В описанном примере изображены скриншоты расчета в ПК ЛИРА 10.6, как очень удобного инструмента по созданию расчетных схем. ПК ЛИРА 10.6 – это одна из немногих программ, которая в демоверсии позволяет выполнить подобный расчет с проверкой сечений металлопроката и подбором армирования плит.
Вы можете скачать файл, где приведены расчеты данной задачи в ПК ЛИРА 10.6.
Скачать файл





.svg)

.svg)








 Заказать обратный звонок
Заказать обратный звонок